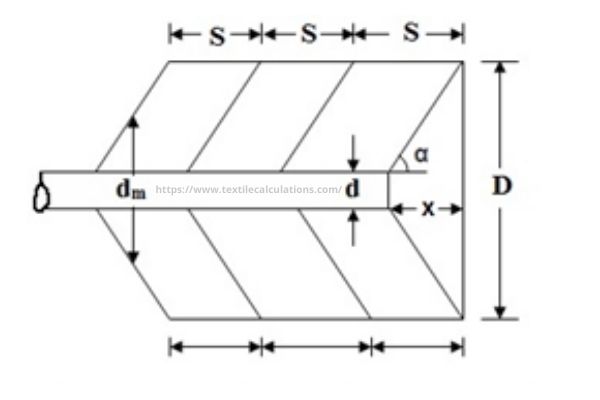
The relation between Taper Angle and Amount of Yarn on a Beam is discussed below:
Let,
s = Traverse length.
L = Axial
d = Empty beam dia.
D = Full beam dia.
Relation between Taper Angle and Amount of Yarn on a Beam is:
dm = (D+d)/2 = mean dia.
Where,
X = Tape distance
α = Taper angle
v = Volume of yarn stored on beam.
Let, s > x so as to maintain stability
…….∏D2L ∏d2L
V = ………. – ………….
……….4…………….4
…..∏L
= …….. (D2 – d2)
……4
………….D+d D-d
= ∏L (………) (……….)
…………….2 . 2
From the figure, it is clear that
……….D+d……..D-d
dm = ……… & ………… = x tan α
…………..2………..2
So, v = π L dm (x tanα)
V > π L dm S tan α if, x > s
V < π L dm S tan α if, x < s
So, V ∞ S tan α if α = 90° then V = α
So unlimited amount of yarns can be wound if the flange stays perpendicular to the beam barrel. Practically this is impossible. But this type of package permit’s wind a high amount of yarn.
You may like also: Relation between Yarn Dia and Yarn Count
Author of this Article: Rofiquzzaman Raju Fabric Technologist, B.J.Group, Mawna, Gazipur Email: [email protected]
